Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
Геометрия пространств со скалярным произведением / Унитарные пространства / 1 2 3 4 5 6 7 8 9 10 11
Унитарные пространства1. Определение. Унитарным пространством называется комплексное линейное пространство L с эрмитовым положительно определенным скалярным произведением. Как в разделе Евклидовы пространства, будем писать (l, m) вместо g(l, m) и | l | вместо (l, l)1/2. Далее убедимся, что | l | является нормой на L в смысле п. 1. Унитарные пространства, полные относительно этой нормы, называются также гильбертовыми. В частности, конечномерные унитарные пространства гильбертовы. Из результатов, доказанных в разделах Теоремы классификации, Алгоритм ортогонализации и ортогональные многочлены, следует, что: а) всякое конечномерное унитарное пространство имеет ортонормированный базис, все векторы которого имеют длину 1; б) поэтому оно изоморфно координатному унитарному пространству Cn (n = dim L) со скалярным произведением
Ряд свойств унитарных пространств близок к свойствам евклидовых, главным образом по следующей причине: если L - конечномерное унитарное пространство, то на его овеществлении LR имеется (единственная) структура евклидова пространства, в которой норма | l | вектора та же, что и в L. Существование видно из предыдущего абзаца: если {e1, ..., en} - ортонормированный базис L, а {e1, ie1, e2, ie2, ..., en, ien} - соответствующий базис LR, то
и выражение справа есть евклидов квадрат нормы вектора |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
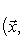
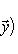
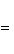
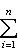
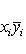
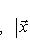
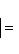
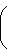
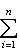
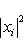
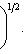
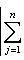
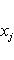

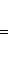
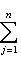
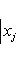
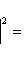
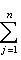
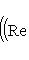
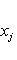
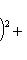


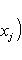
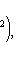
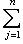
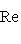
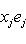
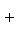
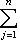
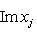
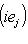 в ортонормированном базисе {ej, iej}. Единственность следует из
в ортонормированном базисе {ej, iej}. Единственность следует из