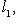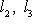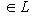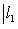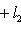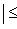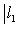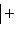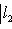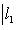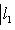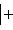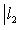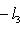Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Унитарные пространства / 1 2 3 4 5 6 7 8 9 10 11
4. Предложение. Для любых
причем равенство достигается тогда и только тогда, когда векторы l1, l2 пропорциональны. Доказательство. Как в п. 2, для любых вещественных t имеем
Случай l1 = 0 тривиален. Считая, что
Но если
Строгое равенство здесь достигается тогда и только тогда, когда В точности так же, как в евклидовом случае, отсюда выводятся следствия: 5. Следствие (неравенство треугольника). Для любых
|
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
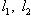
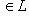

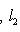
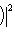
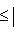
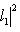
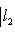
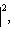
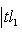
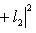
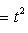
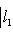
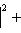
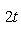
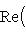
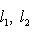
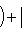

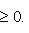
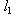
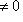 , выводим отсюда, что
, выводим отсюда, что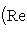
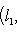
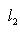
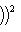
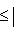
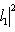
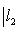
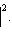
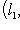
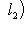
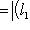
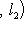
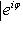
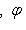
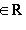 , то
, то 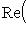
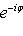
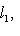
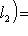
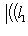
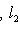
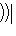 . Поэтому
. Поэтому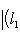

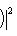
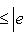
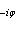
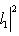
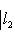
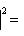
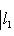
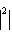
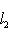
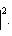
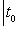
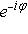
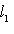
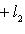
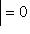 для подходящего
для подходящего 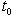
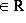 , что завершает доказательство.
, что завершает доказательство.