Геометрия пространств со скалярным произведением / Унитарные пространства / 1 2 3 4 5 6 7 8 9 10 11
а) Унитарное пространство 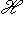 , называемое пространством состояний системы. Такие пространства, рассматриваемые в стандартных учебниках, по большей части являются бесконечномерными гильбертовыми пространствами, которые реализуются как пространства функций на моделях "физического" пространства или пространства-времени. Конечномерные пространства , называемое пространством состояний системы. Такие пространства, рассматриваемые в стандартных учебниках, по большей части являются бесконечномерными гильбертовыми пространствами, которые реализуются как пространства функций на моделях "физического" пространства или пространства-времени. Конечномерные пространства 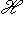 возникают, грубо говоря, как пространства внутренних степеней свободы системы, если она рассматривается как локализованная или если ее движением в физическом пространстве можно так или иначе пренебречь. Таково двумерное унитарное пространство "спиновых состояний" электрона, к которому мы еще вернемся. возникают, грубо говоря, как пространства внутренних степеней свободы системы, если она рассматривается как локализованная или если ее движением в физическом пространстве можно так или иначе пренебречь. Таково двумерное унитарное пространство "спиновых состояний" электрона, к которому мы еще вернемся.
б) Лучи, т. е. одномерные комплексные подпространства в 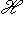 , называются (чистыми) состояниями системы. , называются (чистыми) состояниями системы.
Вся информация о состоянии системы в фиксированный момент времени определяется заданием луча 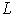 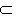 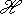 или ненулевого вектора или ненулевого вектора 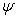 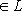 , который называется иногда , который называется иногда 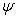 -функцией, отвечающей этому состоянию, или вектором состояния. -функцией, отвечающей этому состоянию, или вектором состояния.
Фундаментальный постулат о том, что 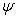 -функции образуют комплексное линейное пространство, называется принципом суперпозиции, а линейная комбинация -функции образуют комплексное линейное пространство, называется принципом суперпозиции, а линейная комбинация 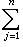 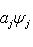 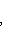 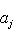 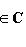 , описывает суперпозицию состояний , описывает суперпозицию состояний 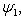 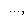 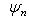 . Заметим, что, поскольку физический смысл имеют только лучи . Заметим, что, поскольку физический смысл имеют только лучи 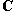 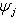 , а не сами векторы , а не сами векторы 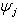 , коэффициентам aj также нельзя приписать однозначно определенного смысла. Однако, если выбирать , коэффициентам aj также нельзя приписать однозначно определенного смысла. Однако, если выбирать 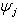 нормированными, нормированными, 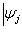 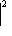 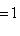 , и линейно независимыми, а также нормировать , и линейно независимыми, а также нормировать 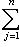 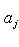 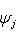 , то произвол в выборе вектора , то произвол в выборе вектора 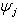 в своем луче сводится к умножениям на числа в своем луче сводится к умножениям на числа 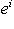 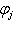 , которые называются фазовыми множителями; таков же будет произвол в выборе коэффициентов aj, которые мы сможем тогда сделать вещественными и неотрицательными, что вместе с условием нормировки , которые называются фазовыми множителями; таков же будет произвол в выборе коэффициентов aj, которые мы сможем тогда сделать вещественными и неотрицательными, что вместе с условием нормировки 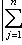 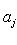 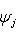 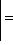 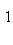 позволяет определить их однозначно. позволяет определить их однозначно.
-1-2-3-4-5-6-7-8-9-10-11-
|
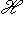 , называемое пространством состояний системы. Такие пространства, рассматриваемые в стандартных учебниках, по большей части являются бесконечномерными гильбертовыми пространствами, которые реализуются как пространства функций на моделях "физического" пространства или пространства-времени. Конечномерные пространства
, называемое пространством состояний системы. Такие пространства, рассматриваемые в стандартных учебниках, по большей части являются бесконечномерными гильбертовыми пространствами, которые реализуются как пространства функций на моделях "физического" пространства или пространства-времени. Конечномерные пространства 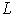
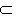
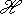 или ненулевого вектора
или ненулевого вектора 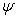
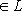 , который называется иногда
, который называется иногда 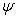 -функцией, отвечающей этому состоянию, или вектором состояния.
-функцией, отвечающей этому состоянию, или вектором состояния.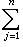
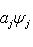
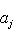
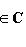 , описывает суперпозицию состояний
, описывает суперпозицию состояний 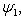
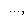
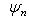 . Заметим, что, поскольку физический смысл имеют только лучи
. Заметим, что, поскольку физический смысл имеют только лучи 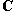
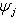 , а не сами векторы
, а не сами векторы 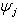 , коэффициентам aj также нельзя приписать однозначно определенного смысла. Однако, если выбирать
, коэффициентам aj также нельзя приписать однозначно определенного смысла. Однако, если выбирать 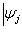
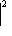
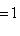 , и линейно независимыми, а также нормировать
, и линейно независимыми, а также нормировать 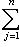
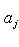
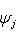 , то произвол в выборе вектора
, то произвол в выборе вектора 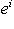
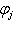 , которые называются фазовыми множителями; таков же будет произвол в выборе коэффициентов aj, которые мы сможем тогда сделать вещественными и неотрицательными, что вместе с условием нормировки
, которые называются фазовыми множителями; таков же будет произвол в выборе коэффициентов aj, которые мы сможем тогда сделать вещественными и неотрицательными, что вместе с условием нормировки 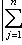
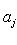
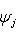
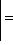
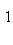 позволяет определить их однозначно.
позволяет определить их однозначно.