Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Категорные свойства линейных пространств / 1 2 3 4 5
3. Теорема о точности функтора а) б) Доказательство. а) Напомним (см. пример г) п. 6), что i1 ставит в соответствие морфизму Мы проверили, что последовательность а) является комплексом, и остается установить ее точность в среднем члене, т. е. Ker j1 = Im i1. Мы уже знаем, что |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
 . Пусть
. Пусть 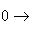
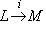
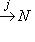
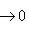 - точная тройка конечномерных линейных пространств, P - любое конечномерное пространство над тем же полем. Тогда
- точная тройка конечномерных линейных пространств, P - любое конечномерное пространство над тем же полем. Тогда 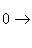
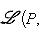
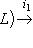
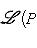
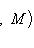
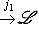
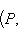
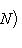
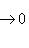 ,
,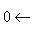
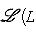
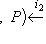
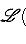
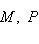
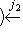
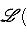
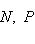
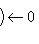 .
.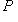
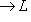 его композицию с
его композицию с 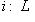
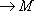 , а j1 ставит в соответствие морфизму
, а j1 ставит в соответствие морфизму 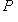
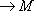 его композицию с
его композицию с 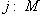
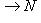 . Отображение i1 инъективно, потому что i - инъекция, так что если композиция
. Отображение i1 инъективно, потому что i - инъекция, так что если композиция 
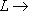
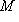 нулевая, то
нулевая, то 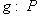
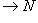 можно поднять до морфизма
можно поднять до морфизма 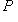
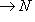 , которая является композицией
, которая является композицией 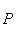
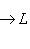
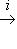

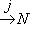 , но ji = 0.
, но ji = 0.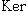
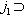
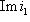 . Для доказательства обратного включения заметим, что если стрелка
. Для доказательства обратного включения заметим, что если стрелка 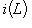
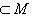 в силу точности исходной тройки. Значит, P отображается в подпространство i), и потому стрелку
в силу точности исходной тройки. Значит, P отображается в подпространство i), и потому стрелку