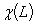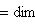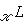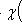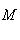
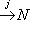
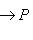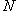
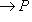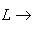
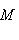
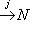
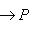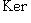
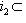
б) Здесь рассуждения совершенно аналогичны, или, точнее, двойственны. Отображение i₂ сюръективно в силу утвеждения б) теоремы п. 2. Отображение j₂ инъективно, потому что если композиция равна нулю, то и стрелка нулевая, так как j сюръективно. Композиция i₂j₂ равна нулю, так как композиция нулевая для любой последней стрелки. Поэтому остается доказать, что 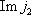(обратное включение только что проверено). 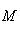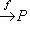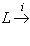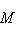Но стрелка лежит в ядре i₂, если композиция 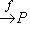нулевая. Значит, L = Ker j лежит в ядре f. 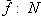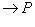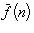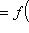Определим отображение формулой 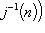, где 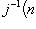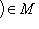- любой прообраз n. От выбора этого прообраза ничего не зависит, так как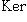 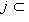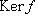. 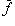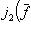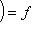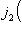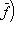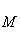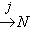Легко проверить, что линейно и что ; в самом деле, есть композиция 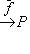, которая переводит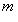 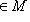в 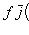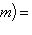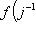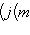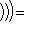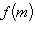. Теорема доказана.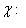

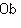
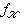
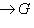4. Категорная характеризация размерности. Пусть G - некоторая абелева группа, записываемая аддитивно, - произвольная функция, определенная на конечномерных линейных пространствах и удовлетворяющая двум условиям: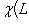

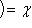
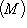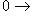
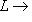
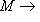
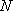
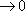а) если L и M изоморфны, то ;

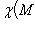
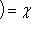
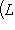
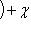
б) для любой точной тройки пространств имеем 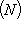(такие функции называются аддитивными).

Имеет место

5. Теорема. Для любой аддитивной функции имеем

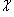где L - произвольное конечномерное пространство.

-1-2-3-4-5-