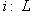
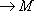б) Пусть P, L, M - линейные пространства, M конечномерно, - инъективное линейное отображение. Тогда любое линейное отображение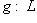 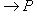можно продолжить до линейного отображения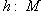 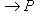так, что g = hi. Другими словами, диаграмму с точной нижней строкой

можно вложить в коммутативную диаграмму

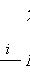
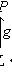
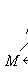
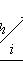
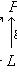
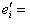
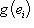
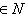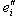
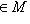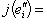
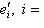
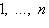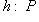
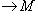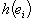
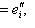
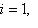
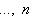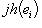
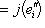
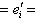
Доказательство. а) Выберем базис {e₁, ..., e_n в P, положим . В силу сюръективности j существуют векторы такие, что . По предложению п. 3, существует единственное линейное отображение такое, что . По конструкции 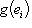. Так как {e_i образуют базис P, имеем jh = g.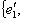

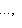
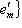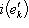
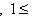
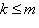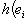
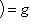
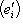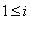
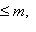
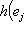
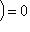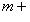
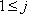
б) Выберем базис пространства L и продолжим , до базиса {e₁, ..., e_m; e_m+1, ..., e_n пространства M. Положим при при 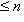. Такое отображение существует по тому же предложению п. 3. Можно также прямо применить предложению п. 8. Теорема доказана.

В категории модулей объекты P, удовлетворяющие условию а) теоремы (при всех M, N) называются проективными, а объекты, удовлетворяющие условию б), - инъективными. Доказали, что в категории конечномерных линейных пространств все объекты проективны и инъективны.

-1-2-3-4-5-