Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Язык категорий / 1 2 3 4 5 6 7 8
в) Операции комплексификации и овеществления определяют функторы г) Для любой категории C и любого объекта X Вот их определения: Аналогично, Проверьте, что hX и hX действительно являются функторами. Их называют функторами, представляющими объект X категории. Заметим, что если C = 7. Композиция функторов. Если Можно ввести "категорию категорий", объектами которой являются категории, а морфизмами - функторы! Более важной является следующая ступень этой высокой лестницы абстракций: категория функторов. Ограничимся объяснением, что такое морфизмы функторов. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
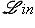

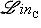 и
и 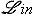
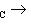
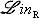 соответственно. То же относится к более общим конструкциям подъема и спуска поля скаляров.
соответственно. То же относится к более общим конструкциям подъема и спуска поля скаляров.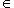 Ob C определены два функтора из C в категорию множеств: ковариантный
Ob C определены два функтора из C в категорию множеств: ковариантный 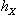
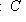
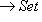 и контравариантный
и контравариантный 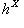
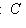
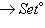 .
.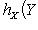
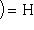
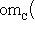
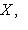
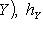
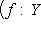
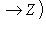 есть отображение
есть отображение 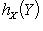
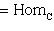
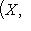
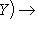
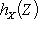
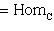
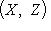 , которое ставит в соответствие морфизму
, которое ставит в соответствие морфизму 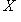
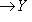 его композицию с морфизмом
его композицию с морфизмом 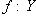
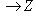 .
.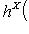
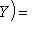
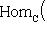
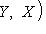 и
и 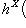
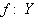
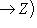 есть отображение
есть отображение 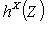
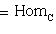
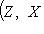
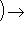
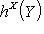
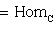
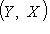 , которое ставит в соответствие морфизму
, которое ставит в соответствие морфизму 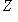
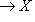 его композицию с морфизмом
его композицию с морфизмом 
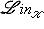 , то hX и hX можно считать функторами со значениями также в
, то hX и hX можно считать функторами со значениями также в 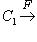
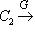
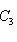 - три категории и два функтора между ними, то композиция
- три категории и два функтора между ними, то композиция 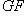
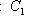
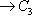 определяется как теоретико-множественная композиция отображений на объектах и морфизмах. Тривиально проверяется, что она является функтором.
определяется как теоретико-множественная композиция отображений на объектах и морфизмах. Тривиально проверяется, что она является функтором.