Линейные пространства и линейные отображения / Язык категорий / 1 2 3 4 5 6 7 8
Тогда коммутативная диаграмма в C
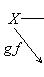 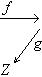 
отвечает коммутативной диаграмме в 
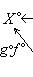  
(Ковариантный) функтор 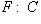 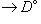 можно отождествить с контравариантным функтором можно отождествить с контравариантным функтором 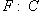 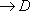 в смысле данного выше определения. в смысле данного выше определения.
6. Примеры. а) Пусть  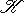 - поле, - поле,  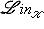 - категория линейных пространств над - категория линейных пространств над  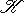 , Set - категория множеств. В разделе Линейные пространства приводится объяснение, как любому множеству S , Set - категория множеств. В разделе Линейные пространства приводится объяснение, как любому множеству S 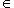 Ob Set поставить в соответствие линейное пространство F(S) Ob Set поставить в соответствие линейное пространство F(S) 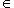 Ob Ob  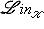 функций на S со значениями в функций на S со значениями в  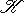 . Поскольку это естественная конструкция, следует ожидать, что она может быть продолжена до функтора. Так оно и есть. Функтор оказывается контравариантным морфизму . Поскольку это естественная конструкция, следует ожидать, что она может быть продолжена до функтора. Так оно и есть. Функтор оказывается контравариантным морфизму 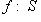 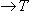 он ставит в соответствие линейное отображение он ставит в соответствие линейное отображение 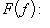 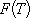 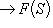 , чаще обозначаемое f* и называемое подъемом, или обратным образом, на функциях: , чаще обозначаемое f* и называемое подъемом, или обратным образом, на функциях:
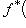 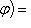 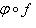 , где , где 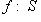 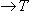 , , 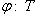 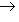 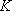 . .
Другими словами, 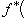 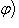 - это функция на S, значения которой постоянны вдоль "слоев" f -1(t) отображения f и равны - это функция на S, значения которой постоянны вдоль "слоев" f -1(t) отображения f и равны 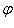 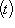 на таком слое. В качестве упражнения - проверить, что действительно построили функтор. на таком слое. В качестве упражнения - проверить, что действительно построили функтор.
б) Отображение двойственности 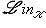 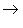 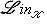 , на объектах задаваемое формулой , на объектах задаваемое формулой 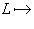 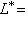 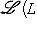 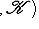 , а на морфизмах - формулой , а на морфизмах - формулой 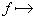 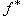 , является контравариантным функтором из категории , является контравариантным функтором из категории  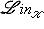 в себя. По существу, это доказано в разделе Двойственность. в себя. По существу, это доказано в разделе Двойственность.
-1-2-3-4-5-6-7-8-
|
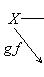
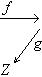

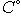
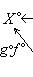


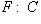
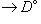 можно отождествить с контравариантным функтором
можно отождествить с контравариантным функтором 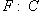
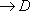 в смысле данного выше определения.
в смысле данного выше определения.
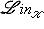 - категория линейных пространств над
- категория линейных пространств над 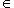 Ob Set поставить в соответствие линейное пространство F(S)
Ob Set поставить в соответствие линейное пространство F(S) 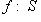
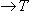 он ставит в соответствие линейное отображение
он ставит в соответствие линейное отображение 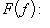
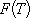
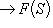 , чаще обозначаемое f* и называемое подъемом, или обратным образом, на функциях:
, чаще обозначаемое f* и называемое подъемом, или обратным образом, на функциях: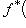
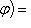
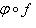 , где
, где 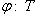
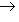
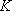 .
.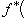
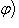 - это функция на S, значения которой постоянны вдоль "слоев" f -1(t) отображения f и равны
- это функция на S, значения которой постоянны вдоль "слоев" f -1(t) отображения f и равны 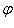
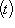 на таком слое. В качестве упражнения - проверить, что действительно построили функтор.
на таком слое. В качестве упражнения - проверить, что действительно построили функтор.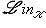
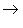
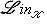 , на объектах задаваемое формулой
, на объектах задаваемое формулой 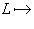
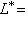
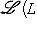
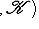 , а на морфизмах - формулой
, а на морфизмах - формулой 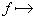
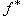 , является контравариантным функтором из категории
, является контравариантным функтором из категории