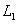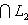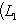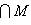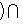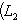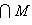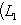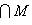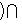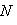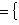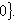Доказательство. Докажем несколько более сильный результат, полезный в приложениях, а именно установим существование подпространства L₂ среди конечного числа изотропных подпространств, связанных с фиксированным симплектическим базисом {e₁, ..., e_r; e_r+1, ..., e_2r в L.

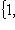
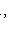
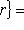
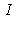
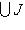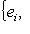
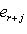
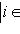
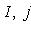
Пусть дано разбиение на два непересекающихся подмножества. Тогда r векторов 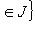порождают r-мерное изотропное подпространство в L, называемое координатным (относительно выбранного базиса). Очевидно, их имеется 2^r. Покажем, что L₂ можно найти среди координатных подпространств.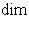

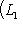
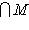
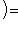
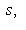
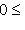
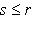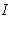
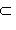
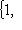
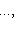
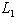
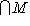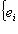
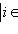
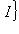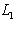
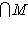
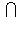
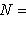
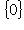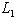
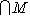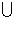
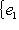
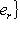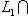
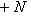
Пусть M натянуто на {e₁, ..., e_r и . Существует такое подмножество из r - s элементов, что трансверсально к N, натянутому на , т. е. . Действительно, множество {базис порождает M, поэтому базис 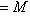можно дополнить до базиса M с помощью r - s векторов из {e₁, ..., e_r по предложению п. 10. Номера этих векторов образуют искомое I, т. к. , так что .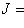

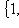
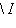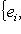
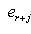
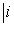
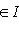
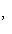
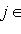
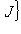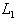
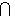
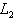
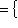
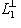
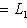
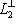
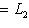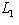
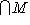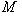
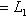
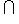
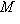
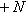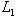
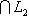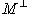
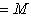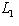
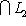
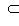
Положим теперь и покажем, что изотропное подпространство L₂, натянутое на , является прямым дополнением к L₁. Достаточно проверить, что . Действительно, из доказательства предложения п. 2 следует, что . Но содержится в L₁, N содержится в L₂, так что сумма ортогональна к . Но M изотропно размерности r, поэтому , и 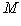. Значит, окончательно

-1-2-3-4-5-6-7-8-