Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Симплектические пространства / 1 2 3 4 5 6 7 8
Доказательство. Поскольку форма [ , ] невырождена, она определяет изоморфизм Рассмотрим теперь ограничение формы [ , ] на
с матрицей Грама
Размер единичной клетки есть 3. Предложение. Пусть L - симплектическое пространство размерности 2r, |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

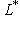 , при котором вектору
, при котором вектору 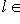
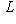 ставится в соответствие линейный функционал
ставится в соответствие линейный функционал 

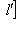 . Отсюда следует, что для любого подпространства
. Отсюда следует, что для любого подпространства 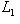
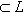 имеем
имеем 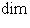

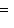
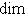
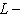

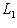 . Если к тому же L1 изотропно, то
. Если к тому же L1 изотропно, то 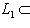
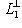 , откуда
, откуда 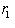
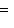
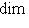
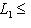
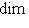
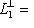
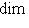
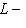
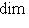
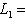
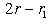 , так что
, так что 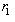
 .
.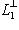 . Во всем пространстве L ортогональное дополнение к
. Во всем пространстве L ортогональное дополнение к 
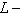
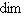
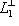
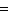
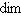
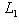 по предыдущему рассуждению. С другой стороны, L1 лежит в этом ортогональном дополнении и потому совпадает с ним. Значит, L1 есть в точности ядро ограничения [ , ] на
по предыдущему рассуждению. С другой стороны, L1 лежит в этом ортогональном дополнении и потому совпадает с ним. Значит, L1 есть в точности ядро ограничения [ , ] на 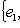
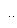

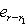
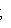
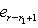
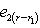

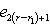
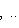
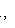
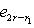
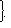
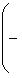
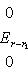
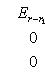
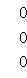
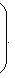
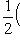
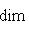
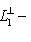
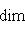
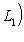
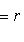
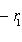 . Векторы
. Векторы 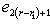
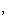
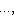

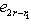 порождают ядро формы на
порождают ядро формы на 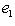
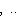

 , получим r-мерное изотропное подпространство, содержащее L1.
, получим r-мерное изотропное подпространство, содержащее L1.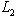
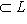 размерности r такое, что
размерности r такое, что 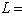
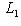
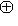
 , и скалярное произведение индуцирует изоморфизм
, и скалярное произведение индуцирует изоморфизм 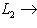
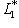 .
.