Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Базис и размерность / 1 2 3 4 5 6 7 8 9 10 11
Доказательство. a) Если б) Если Пусть E = {e1, ..., en} - некоторое конечное семейство векторов в L, F = {ei1, ..., eim} - его линейно независимое подсемейство. Назовем F максимальным, если каждый элемент из E линейно выражается через элементы из F. 10. Предложение. Каждое линейно независимое подсемейство Доказательство. Если в В случае |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
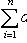
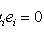 и
и 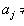
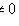 , то
, то 
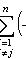
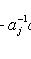
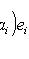 . Наоборот, если
. Наоборот, если 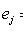
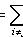
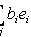 , то
, то 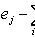
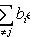
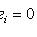 .
.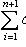
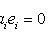 не все ai равны нулю, то обязательно
не все ai равны нулю, то обязательно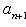
 , иначе мы получили бы нетривиальную линейную зависимость между e1, ..., en. Поэтому
, иначе мы получили бы нетривиальную линейную зависимость между e1, ..., en. Поэтому 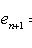
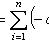
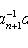
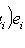 . Лемма доказана.
. Лемма доказана.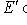
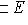 содержится в некотором максимальном линейно независимом подсемействе
содержится в некотором максимальном линейно независимом подсемействе 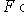
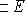 . Линейные оболочки F и E совпадают.
. Линейные оболочки F и E совпадают.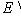
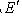 есть вектор, не представимый в виде линейной комбинации элементов
есть вектор, не представимый в виде линейной комбинации элементов 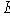
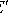 , добавим его к
, добавим его к 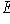
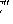 будет линейно независимым. Применим то же рассуждение к
будет линейно независимым. Применим то же рассуждение к 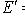
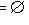 в качестве
в качестве