Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Базис и размерность / 1 2 3 4 5 6 7 8 9 10 11
11. Замечание. Этот результат верен и для бесконечных семейств Е. Для его доказательства следует применить трансфинитную индукцию или лемму Цорна. Максимальное подсемейство не обязательно единственно: рассмотрим E = {(1, 0), (0, 1), (1, 1)}, 12. Теорема о продолжении базиса. Пусть Доказательство. Выберем какой-нибудь базис {em+1, ..., en} в L и положим E = {e1, ..., em, em+1, ..., en}. Обозначим через F максимальное линейно независимое подсемейство E, содержащее В самом деле, нужно только проверить, что линейная оболочка F совпадает с L. Но она равна линейной оболочке E по предложению п. 10, а последняя равна L, потому что в E содержится базис пространства L. 13. Следствие (монотонность размерности). Пусть M - линейное подпространство в L. Тогда Доказательство. Если M бесконечномерно, то L также бесконечномерно. Действетельно, покажем сначала, что в M можно найти сколь угодно большие независимые семейства векторов. Если семейство из n линейно независимых векторов {e1, ..., en} уже найдено, то его линейная оболочка |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
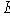
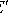 = {(1, 0)} в
= {(1, 0)} в 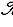
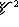 . Тогда
. Тогда 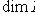
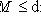
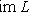 , и если L конечномерно, то из dim M = dim L следует, что M = L.
, и если L конечномерно, то из dim M = dim L следует, что M = L.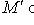
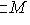 не может совпадать с M - иначе M было бы n-мерно.
не может совпадать с M - иначе M было бы n-мерно.