Поэтому в M есть вектор e_n+1, линейно не выражающийся через {e₁, ..., e_n, и утверждение б) леммы п. 9 показывает, что семейство {e₁, ..., e_n, e_n+1 линейно независимо. Теперь предположим, что M бесконечномерно, а L n-мерно. Тогда любые n + 1 линейных комбинаций элементов базиса L линейно зависимы по рассуждению в доказательстве теоремы п. 4, что противоречит бесконечномерности M.

Остается разобрать случай, когда M и L конечномерны. Но тогда любой базис M по теореме п. 12 можно продолжить до базиса L, откуда и следует, что .

Наконец, если dim M = dim L, то любой базис M должен быть базисом L - иначе его продолжение до базиса состояло бы из > dim L элементов, что невозможно.

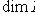
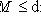
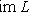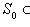
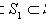
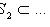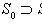
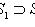
14. Базисы и флаги. Один из стандартных способов изучения множеств S с алгебраическими структурами состоит в выделении в них последовательности подмножеств или 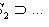так, что переход от одного подмножества к следующему устроен в каком-то смысле просто. Общее название таких последовательностей - фильтрации (возрастающая и убывающая соответственно). В теории линейных пространств строго возрастающая последовательность подпространств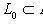 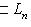пространства L называется флагом. 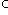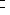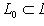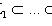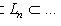(Мотивировка названия: флаг {точка 0{прямая{плоскость - это "гвоздь", "древко" и "полотнице".)

Число n назовем длиной флага .

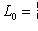
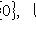
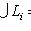
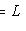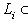
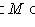
Флаг назовем максимальным, если и между L_i, L_i+1 (для всех i) нельзя вставить подпространство: если 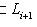, то либо L_i = M, либо M = L_i+1.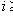

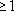По всякому базису {e₁, ..., e_n пространства L можно построить флаг длины n, положив L₀ = {0, L_i - линейная оболочка {e₁, ..., e_i (при ). Из доказательства следующей теоремы будет видно, что этот флаг максимален и что наша конструкция дает все максимальные флаги.

-1-2-3-4-5-6-7-8-9-10-11-