Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
11. Нормальные операторы. Как унитарные, так и самосопряженные операторы в унитарном пространстве являются частным случаем нормальных операторов, которые можно описать двумя равносильными свойствами: а) Это операторы, диагонализируемые в ортонормированном базисе. б) Это операторы, коммутирующие со своим сопряженным оператором. Проверим равносильность. Если {ei} - ортонормированный базис с Для доказательства обратной импликации выберем собственное значение
Проверим, что
поскольку ff* = f*f. Отсюда вытекает, что пространство (f(l), l0) = (l, f*(l0)) = 0. Такое же рассуждение показывает, что -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
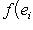
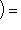
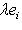 , то
, то 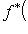
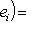
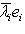 , так что [f, f*] = 0, и из а) следует б).
, так что [f, f*] = 0, и из а) следует б).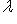 оператора f и положим
оператора f и положим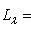
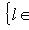
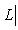
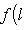
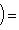
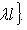
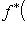
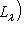
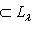 . В самом деле, если
. В самом деле, если 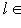
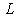 , то
, то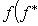
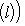
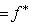
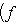
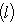
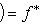
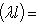
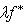
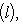
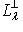 f-инвариантно: если (l, l0) = 0 для всех
f-инвариантно: если (l, l0) = 0 для всех 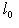
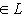 , то
, то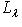 , это завершает доказательство.
, это завершает доказательство.