Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Формула (3) определяет операцию (формального) сопряжения дифференциальных операторов: Если скалярное произведение определяется с помощью веса G(x):
то очевидные вычисления показывают, что вместо D* следует рассматривать оператор Покажем, что ортогональные системы функций, рассмотренные в разделе Алгоритм ортогонализации и ортогональные многочлены, состоят из собственных функций самосопряженных дифференциальных операторов. а) Вещественные многочлены Фурье степени -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
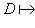
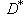 . Оператор D называется (формально) самосопряженным, если D = D*. Слово "формальный" здесь напоминает о том, что в определении не указано явно пространство, на котором D реализуется как линейный оператор.
. Оператор D называется (формально) самосопряженным, если D = D*. Слово "формальный" здесь напоминает о том, что в определении не указано явно пространство, на котором D реализуется как линейный оператор.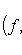
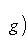
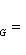


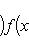
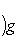
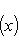
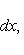
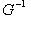

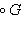 (считая, что G не обращается в нуль); именно он является кандидатом на роль сопряженного оператора к D относительно (f, g)G.
(считая, что G не обращается в нуль); именно он является кандидатом на роль сопряженного оператора к D относительно (f, g)G.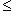
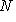 . Оператор
. Оператор 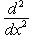 , формально самосопряженный, переводит это пространство в себя и самосопряжен на нем. Кроме того, его собственные значения равны 0 (кратность 1) и -12, -22, ..., - N2 (кратность 2). Соответствующие собственные векторы суть 1 и
, формально самосопряженный, переводит это пространство в себя и самосопряжен на нем. Кроме того, его собственные значения равны 0 (кратность 1) и -12, -22, ..., - N2 (кратность 2). Соответствующие собственные векторы суть 1 и 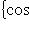

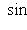
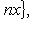
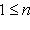
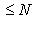 .
.