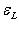
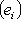В самом деле, согласно определению есть функционал на L^*, значение которого на e^k равно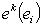 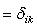("символ Кронекера"). Но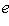 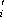- точно такой же функционал на L^* по определению двойственного базиса.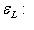

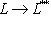Заметим, что если L бесконечномерно, то остается инъективным, но перестает быть сюръективным. В функциональном анализе вместо L^* обычно рассматривают только подпространство линейных функционалов L', непрерывных в подходящей топологии на L и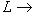 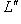, и тогда отображение может быть определено и иногда оказывается изоморфизмом. Такие (топологические) пространства называют рефлексивными. Мы доказали, что конечномерные пространства (без учета топологии) рефлексивны.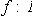

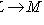Рассмотрим теперь связь между линейными отображениями и линейными подпространствами.

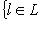
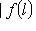
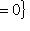
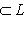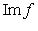
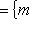
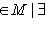
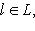
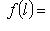
11. Определение. Пусть - линейное отображение. Множество Ker f = называется ядром f, а множество назвывается образом f.

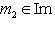
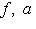
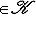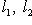
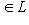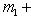
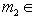
Нетрудно убедиться, что ядро f является линейным подпространством в L, а образ f - линейным подпространством в M. Проверим, например, второе утверждение. Пусть . Тогда существуют такие векторы , что f(l₁) = m₁, m₂. Значит, m₁ + m₂ = f(l₁ + l₂), am₁ = f(al₁). Следовательно, 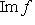и .

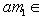
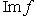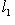
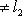Отображение f инъективно тогда и только тогда, когда Ker f = {0. В самом деле, если f(l₁) = f(l₂), , то 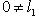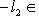Ker f. Наоборот, если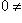 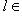Ker f, то f(l) = 0 = f (0).

-1-2-3-4-5-6-7-8-9-