10. Канонический изоморфизм между пространством и дважды двойственным к нему. Пусть L - линейное пространство, L^* - пространство линейных функций на нем, L^** = (L^*)^* - пространство линейных функций на L^* - "дважды двойственное к L пространство".

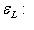
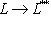Опишем каноническое отображение , не зависящее ни от каких произвольных выборов. Оно ставит в соответствие каждому вектору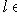 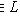функцию на L^*, значение которой на функционале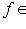 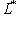равно f(l); в краткой записи: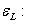

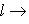
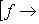
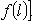
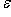
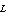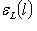
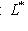
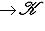Проверим следующие свойства :

а) Для каждого отображение линейно. Действительно, это означает, что выражение f(l) как функция от f при фиксированном l линейно по f. Но это следует из правил сложения функционалов и умножения их на скаляр.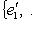

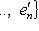Следовательно, действительно определяет отображение L в L^**, как и утверждалось.

б) Отображение линейно. Действительно, это означает, что выражение f(l) как функция от l при фиксированном f линейно, - это так, потому что .

в) Если L конечномерно, то отображение является изоморфизмом. В самом деле, пусть {e₁, ..., e_n - базис L, {e¹, ..., eⁿ - двойственный базис L^*, - базис в L^**, двойственный к {e¹, ..., eⁿ.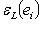

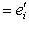Покажем, что , откуда и будет следовать, что - изоморфизм (в этой проверке использование базиса L безобидно, т. к. в определении он не участвовал).

-1-2-3-4-5-6-7-8-9-