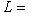
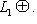
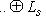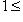
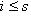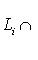
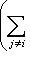
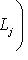
в) . Действительно, выберем и проверим, что 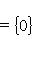. Пусть l - вектор из этого пересечения. Тогда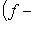

, ;

, .

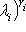
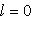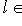
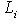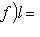
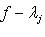
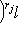
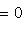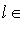
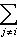
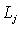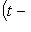
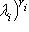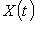
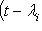
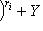
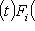
Так как и F_i(t) - взаимно простые многочлены, существуют такие многочлены X(t) и Y(t), что 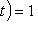. Подставляя сюда f вместо t и применяя полученное операторное тождество к l, находим X(f)(0) + Y(f)(0) = l = 0.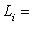

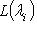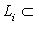
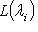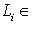
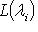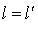
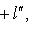
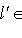
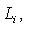
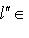
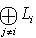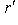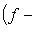
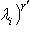
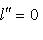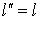
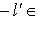
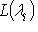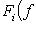
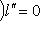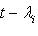
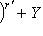
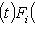
г) . В самом деле, мы уже проверили, что . Для доказательства обратного включения выберем вектор и представим его в виде . Существует такое число , что , поскольку . Кроме того, . Написав тождество 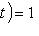, подставив в него f вместо t и применив к 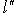, получим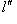 , так что .

6. Следствие. Если оператор f имеет простой спектр, то он диагонализируем.

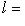
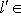
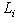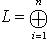
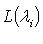Доказательство. В самом деле, число разных собственных значений f тогда равно n = deg P(t) = dim L. Поэтому в разложении все пространства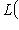 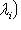одномерны, а так как каждое из них содержит собственный вектор, в базисе из этих векторов матрица оператора f становится диагональной.

-1-2-3-4-5-6-7-8-9-10-