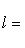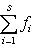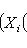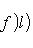Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Жорданова нормальная форма / 1 2 3 4 5 6 7 8 9 10
Доказательство. Допустим, Если 5. Предложение. Доказательство. Пусть а) б) L = L1 + ... + Ls. Действительно, так как многочлены Fi(t) в совокупности взаимно простые, существуют такие многочлены Xi(t), что
Применяя это тождество к любому вектору
|
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
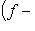
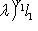
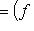
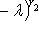
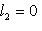 . Полагая r = max(r1, r2), находим
. Полагая r = max(r1, r2), находим 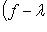
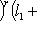
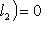 и
и 
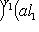
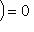 . Следовательно,
. Следовательно, 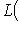
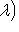 является линейным подпространством.
является линейным подпространством.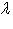 - собственное значение для f, то имеется собственный вектор, отвечающий
- собственное значение для f, то имеется собственный вектор, отвечающий 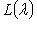
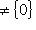 . Наоборот, пусть
. Наоборот, пусть 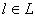
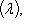
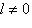 . Выберем наименьшее значение r, для которого
. Выберем наименьшее значение r, для которого 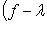
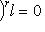 . Очевидно,
. Очевидно, 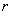
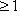 . Вектор
. Вектор 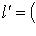
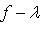
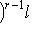 является собственным для f с собственным значением
является собственным для f с собственным значением 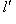
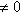 по выбору r и
по выбору r и 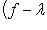
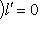 , откуда
, откуда 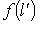
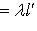 .
.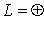
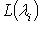 , где
, где 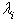 пробегает все собственные значения оператора f, т. е. различные корни характеристического многочлена f.
пробегает все собственные значения оператора f, т. е. различные корни характеристического многочлена f.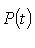

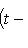
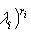 - характеристический многочлен
- характеристический многочлен 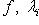
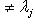 при
при 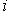
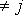 . Положим
. Положим 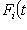

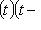
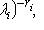
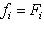
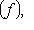
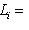
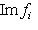 . Проверим следующую серию утверждений.
. Проверим следующую серию утверждений.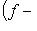
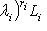
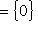 , т. е.
, т. е. 
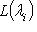 . Действительно,
. Действительно, 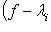
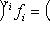
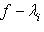

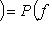
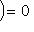 по теореме Гамильтона-Кэли.
по теореме Гамильтона-Кэли.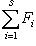
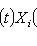
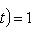 . Поэтому, подставляя вместо t оператор f, имеем
. Поэтому, подставляя вместо t оператор f, имеем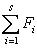
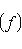
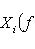
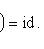
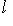
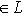 , находим
, находим