Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Матрицы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
10. Классические алгебры Ли. (Матричной) алгеброй Ли называется любая аддитивная подгруппа квадратных матриц Mn( a) Алгебра gl(n, б) Алгебра sl(n, в) Алгебра о(n, Если At = -A, Bt = -B, то [A, B]t = [Bt, At] = [-B, -A] = - [A, B], так что [A, B] кососимметрична. Такие матрицы образуют линейное пространство над Попутно заметим, что матрица A называется симметричной, если At = A. Множество таких матриц не замкнуто относительно коммутирования, но замкнуто относительно антикоммутирования AB + BA или операции Йордана -1-2-3-4-5-6-7-8-9-10-11-12-13-14-15- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
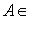
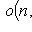
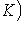 .
.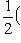
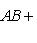
 .
.