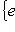
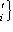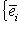
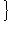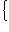
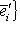Особенно важен частный случай N = M, {e_i = , = , B = C. Матрица линейного оператора f в новом базисе равна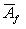

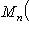
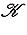
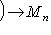
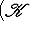
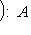
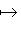
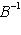
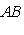Отображение называется сопряжением (посредством невырожденной матрицы B). Сопряжение является автоморфизмом матричной алгебры M_n ():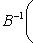

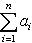
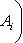
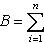
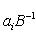
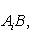
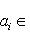
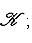
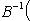
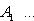
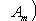
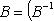
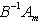
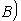
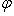(в произведении справа внутренние сомножители B и B ^-1 попарно сокращаются, т. к. стоят рядом).

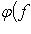
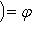
Особую роль играют те функции от элементов M_n (), которые не меняются при замене матрицы на сопряженную, потому что с помощью этих функций можно строить инварианты линейных операторов: если - такая функция, то, полагая 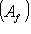, получим результат, зависящий лишь от f, но не от базиса, в котором пишется A_f.

-1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-