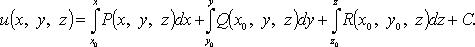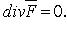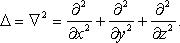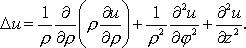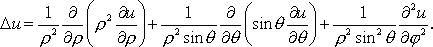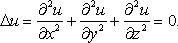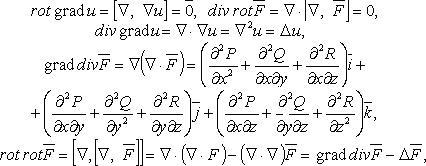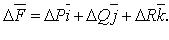Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
|
Формулы / Элементы теории поля / Векторное поле / 1 2 3 4
Векторное поле
Соленоидальное векторное поле Векторное поле Оператор Лапласа
Оператор Лапласа в цилиндрических координатах
Оператор Лапласа в сферических координатах
Уравнение Лапласа
Функции, удовлетворяющие уравнению Лапласа, называются гармоническими. Операции второго порядка
где |
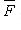 - потенциальное, если
- потенциальное, если 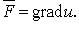 Функция u называется потенциалом
векторного поля
Функция u называется потенциалом
векторного поля 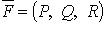 потенциально в односвязной области тогда и только тогда, когда
потенциально в односвязной области тогда и только тогда, когда 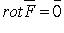 или
или 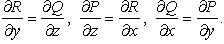 Потенциал в этом случае можно найти, например, по формуле
Потенциал в этом случае можно найти, например, по формуле