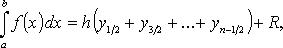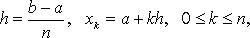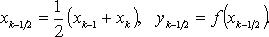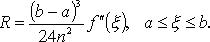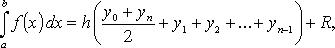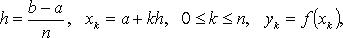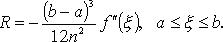Cправочник математических формул
Примеры и задачи с решениями
Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
|
Формулы / Интегральное исчисление / Определенный интеграл / 1 2 3 4 5 6 7 8
Второй случай часто можно свести к первому подходящей заменой переменных. Отметим также, что
Неравенства Если интегралы существуют, то (при a < b) из
Если
Если функция y = f(x) на интервале [a, b] неотрицательна, то интеграл Функция f (x), ограниченная на ограниченном замкнутом интервале [a, b], интегрируема на нем в смысле Римана в том и только в том случае, если она непрерывна почти всюду на [a, b]. Это, в частности, верно: 1) если функция f(x) непрерывна на [a, b]; 2) если функция f(x) ограничена на [a, b] и имеет на [a, b] конечное или счетное множество точек разрыва; 3) если функция f(x) монотонна на [a, b]; 4) если f(x) есть функция ограниченной вариации на [a, b]. Если функция f(x) интегрируема на [a, b], то она интегрируема и на каждом интервале, содержащемся в [a, b]. Приближенное вычисление интегралов Формула средних прямоугольников
Формула трапеций
|
на [a, b] следует
на ограниченном интервале [a, b], то из существования интеграла 
вытекает и существование интеграла 
и
, то интеграл выражает эту площадь, взятую со знаком минус.
