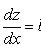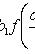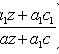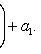Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
|
Формулы / Дифференциальные уравнения / Нелинейные дифференциальные уравнения / 1 2 3 4
Функция
если уравнение
есть уравнение в полных дифференциалах. Интегрирующий множитель удовлетворяет уравнению
Если Аналогично, если Однородное уравнение
где P(x, y), Q(x, y) - однородные функции одной и той же степени Подстановка y = ux, dy = xdu + udx переводит однородное уравнение в линейное относительно функции u:
Уравнение вида 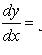 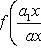 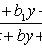 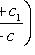
1. Если прямые
2. Если прямые
|
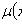
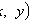 называется интегрирующим множителем для уравнения
называется интегрирующим множителем для уравнения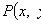
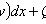
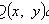
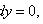
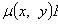
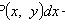
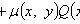
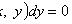
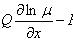
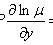
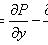
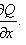
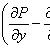
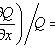
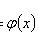 (не зависит от y), то
(не зависит от y), то 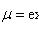
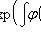
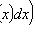 .
.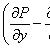
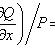
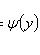 (не зависит от x), то
(не зависит от x), то 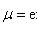
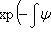
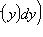 .
.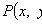
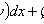
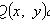
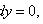
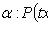
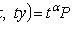
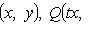
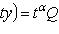
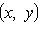 .
.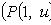
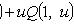
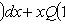
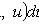
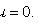
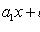
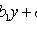
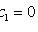 и
и 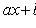
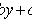
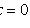 пересекаются в точке (x0; y0), то замена
пересекаются в точке (x0; y0), то замена 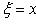
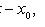
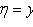
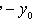 приводит его к однородному уравнению
приводит его к однородному уравнению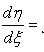
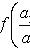
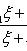
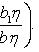
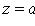
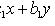 приводит к уравнению с разделяющимися переменными
приводит к уравнению с разделяющимися переменными