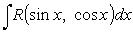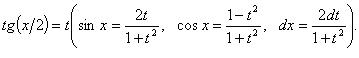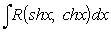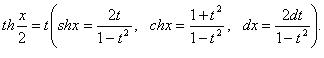Cправочник математических формул
Примеры и задачи с решениями
Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
|
Формулы / Интегральное исчисление / Неопределенный интеграл / 1 2 3 4 5 6 7 8
См. также Неопределенные интегралы
рационализуется лишь в трех случаях: 1) 2) 3) Интегрирование рационально-тригонометрических функций
всегда рационализует универсальная подстановка Специальные подстановки 1) Если R (-sin x, cos x) = -R (sin x, cos x), то рационализует подстановка cos x = t. 2) Если R (sin x, -cos x) = -R (sin x, cos x), то рационализует подстановка sin x = t. 3) Если R (-sin x, -cos x) = R (sin x, cos x), то рационализует подстановка tg x = t. Интегрирование рационально-гиперболических функций
рационализует подстановка |
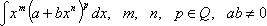
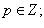подстановка 
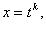где k - общий знаменатель m и n;
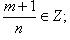подстановка 
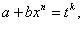где k - знаменатель p;
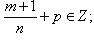подстановка 
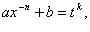где k - знаменатель p.
