Геометрия пространств со скалярным произведением / Трехмерное евклидово пространство / 1 2 3 4 5 6 7 8 9 10 11 12 13
Поэтому x, y должны удовлетворять еще условию  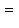 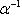 ; тогда автоматически ; тогда автоматически 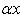 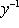 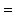 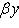 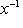 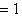 . Можно положить, например, . Можно положить, например, 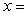 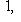 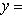 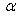 . .
Итак, в базисе {h1, h2} имеем 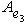 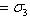 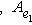 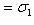 , и этот базис определен с точностью до умножения на скаляр, по модулю равный единице. Те же рассуждения, что для e1, показывают, что в таком базисе , и этот базис определен с точностью до умножения на скаляр, по модулю равный единице. Те же рассуждения, что для e1, показывают, что в таком базисе 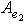 имеет вид имеет вид 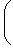 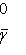 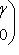 , где , где 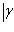  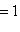 . Кроме того, условие ортогональности e1e2 + e2e1 = 0 дает . Кроме того, условие ортогональности e1e2 + e2e1 = 0 дает
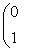 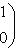 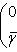  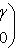 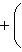 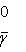 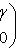 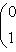  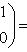 
т. е. 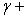 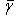 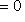 , откуда , откуда 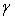 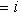 , либо , либо 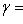 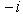 . Поэтому . Поэтому 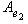 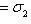 или или 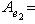 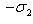 . .
8. Следствие. Пространство 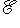 снабжено отмеченной ориентацией: ортонормированный базис {e1, e2, e3} принадлежит к классу, отвечающему этой ориентации, тогда и только тогда, когда существует ортонормированный базис {h1, h2} в снабжено отмеченной ориентацией: ортонормированный базис {e1, e2, e3} принадлежит к классу, отвечающему этой ориентации, тогда и только тогда, когда существует ортонормированный базис {h1, h2} в 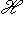 , в котором , в котором 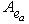 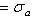 , a = 1, 2, 3. , a = 1, 2, 3.
Доказательство. Мы должны проверить, что если {ea} в базисе {hb} и 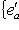 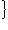 в базисе в базисе 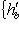 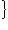 задаются в точности матрицами Паули, то определитель матрицы перехода от {ea} к задаются в точности матрицами Паули, то определитель матрицы перехода от {ea} к 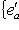 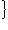 положителен, или что имеется непрерывное движение, переводящее {ea} в положителен, или что имеется непрерывное движение, переводящее {ea} в 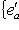 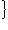 . Построим такое движение, показав, что {hb} переводится в . Построим такое движение, показав, что {hb} переводится в 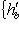 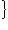 унитарным непрерывным движением: существует такая система унитарных операторов унитарным непрерывным движением: существует такая система унитарных операторов 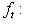 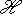 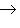 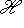 , зависящая от параметра , зависящая от параметра 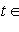 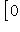 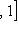 , что , что 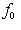 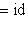  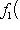 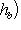  и {ft(h1), ft(h2)} образуют ортонормированный базис и {ft(h1), ft(h2)} образуют ортонормированный базис 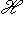 для всех t. Тогда, обозначив через {gt(e1), gt(e2), gt(e3)} ортонормированный базис для всех t. Тогда, обозначив через {gt(e1), gt(e2), gt(e3)} ортонормированный базис 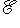 , задающийся матрицами Паули в базисе {ft(h1), ft(h2)}, построим нужное нам движение в , задающийся матрицами Паули в базисе {ft(h1), ft(h2)}, построим нужное нам движение в 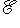 . .
-1-2-3-4-5-6-7-8-9-10-11-12-13-
|

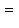
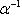 ; тогда автоматически
; тогда автоматически 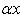
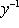
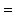
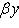
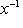
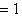 . Можно положить, например,
. Можно положить, например, 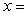
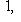
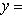
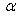 .
.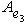
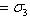
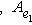
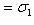 , и этот базис определен с точностью до умножения на скаляр, по модулю равный единице. Те же рассуждения, что для e1, показывают, что в таком базисе
, и этот базис определен с точностью до умножения на скаляр, по модулю равный единице. Те же рассуждения, что для e1, показывают, что в таком базисе 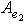 имеет вид
имеет вид 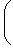
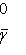
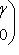 , где
, где 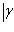

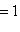 . Кроме того, условие ортогональности e1e2 + e2e1 = 0 дает
. Кроме того, условие ортогональности e1e2 + e2e1 = 0 дает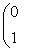
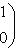
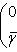

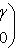
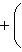
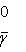
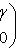
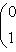

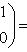

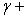
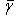
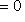 , откуда
, откуда 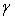
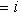 , либо
, либо 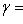
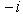 . Поэтому
. Поэтому 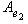
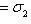 или
или 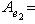
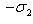 .
.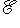 снабжено отмеченной ориентацией: ортонормированный базис {e1, e2, e3} принадлежит к классу, отвечающему этой ориентации, тогда и только тогда, когда существует ортонормированный базис {h1, h2} в
снабжено отмеченной ориентацией: ортонормированный базис {e1, e2, e3} принадлежит к классу, отвечающему этой ориентации, тогда и только тогда, когда существует ортонормированный базис {h1, h2} в 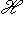 , в котором
, в котором 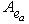
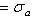 , a = 1, 2, 3.
, a = 1, 2, 3.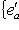
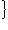 в базисе
в базисе 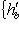
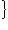 задаются в точности матрицами Паули, то определитель матрицы перехода от {ea} к
задаются в точности матрицами Паули, то определитель матрицы перехода от {ea} к 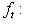
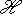
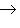
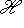 , зависящая от параметра
, зависящая от параметра 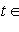
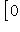
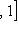 , что
, что 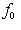
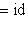

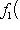
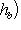
 и {ft(h1), ft(h2)} образуют ортонормированный базис
и {ft(h1), ft(h2)} образуют ортонормированный базис