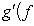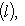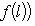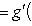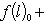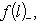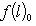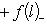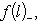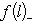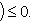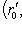
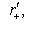
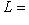
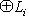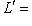
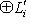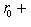
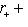
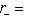
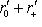
б) Пусть теперь (L, g) и (L', g') - пара ортогональных пространств над R или эрмитовых над C с сигнатурами (r₀, r₊, r_-) и , определенными с помощью некоторых ортогональных разложений , , как в теореме п. 3. Предположим, что между ними существует изометрия. Тогда прежде всего dim L = dim L', так что 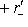. Далее, точно так же, как в предыдущем пункте, проверяется, что r₀ совпадает с размерностью ядра g, а 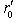- с размерностью ядра g', а эти ядра суть суммы нулевых пространств L_i и 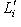в соответствующих разложениях. Поскольку изометрия определяет линейный изоморфизм между ядрами, имеем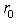 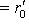и .

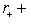
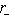
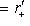
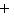
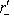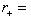
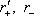
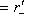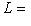
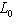
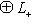
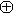
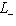
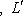
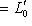
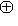
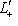
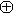
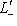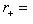
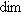
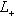
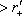
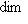
Остается проверить, что . Положим , где L₀, L₊, L_- - суммы нулевых, положительных и отрицательных подпространств исходного разложения L, и соответственно для L'. Предположим, что , и придем к противоречию; возможность 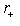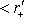разбирается аналогично. Ограничим изометрию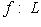 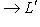на 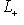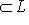. Каждый вектор f(l) однозначно представляется в виде суммы

f(l) = f(l)₀ + f(l)₊ + f(l)_-,

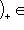
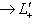
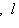
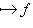
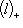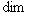
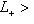
где и т. п. Отображение линейно. Так как по предположению 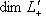, существует ненулевой вектор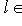 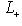, для которого f(l)₊ = 0, так что

f(l) = f(l)₀ + f(l)_-.

Но g(l, l) > 0, потому что и L₊ есть ортогональная прямая сумма положительных одномерных пространств. Так как f - изометрия, мы должны иметь также g'(f(l), f(l)) > 0. С другой стороны,

-1-2-3-4-5-6-7-8-9-10-11-12-13-