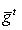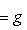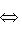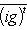Действительно,

Мы будем заниматься почти исключительно скалярными произведениями, которые удовлетворяют одному из следующих условий симметрии относительной этой операции:

а) g^t = g. Такие скалярные произведения называются симметричными, а геометрия пространств с симметричным скалярным произведением называется ортогональной геометрией. Симметричные скалярные произведения задаются симметричными матрицами Грама G.

б) g^t = - g. Такие скалярные произведения называются антисимметричными, или симплектическими, а соответствующие геометрии называются симплектическими. Им отвечают антисимметричные матрицы Грама.

Полуторалинейный случай:

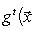
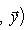
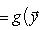
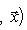
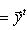
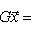
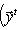
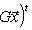
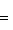
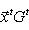
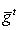
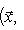
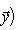
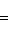
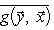
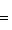
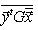
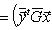
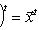
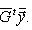
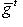
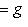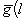
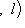
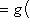
в) . Такие скалярные произведения называются эрмитово симметричными, или просто эрмитовыми, а соответствующие геометрии - эрмитовыми. Им отвечают эрмитовы матрицы Грама. Из условия 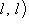следует, что для всех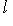 , т. е. все значения g(l, l) вещественны.

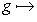
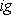Эрмитово антисимметричные скалярные произведения обычно не рассматриваются специально, т. к. отображение устанавливает биекцию между ними и эрмитово симметричными скалярными произведениями:

-1-2-3-4-5-6-7-8-9-10-11-