Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Подпространства и прямые суммы / 1 2 3 4 5 6 7 8 9
7. Определение. Пространство L является прямой суммой своих подространств L1, ..., Ln, если каждый вектор Когда условия определения выполнены, мы пишем 8. Теорема. Пусть а) б) Доказательство. а) Однозначность представления любого вектора |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
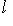
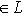 однозначно представляется в виде
однозначно представляется в виде 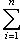
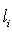 , где
, где 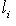
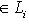 .
.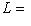
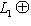
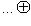
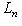 , или
, или 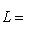
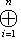
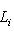 . Например, если {e1, ..., en} - базис L, а
. Например, если {e1, ..., en} - базис L, а 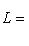
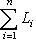 - линейная оболочка вектора ei, то
- линейная оболочка вектора ei, то 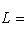
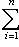
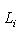 ; последнее условие является более слабым.
; последнее условие является более слабым.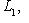
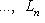 - подпространства в L.
- подпространства в L. 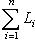
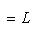 и
и 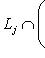
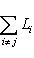
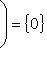 для всех
для всех 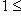
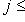
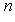 ;
;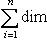

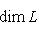 (здесь предполагается, что L конечномерно).
(здесь предполагается, что L конечномерно).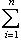
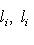
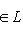 , равносильна однозначности такого представления для нулевого вектора. В самом деле, если
, равносильна однозначности такого представления для нулевого вектора. В самом деле, если 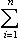
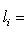
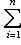
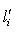 , то
, то 
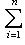
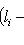
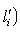 , и наоборот. Если имеется нетривиальное представление
, и наоборот. Если имеется нетривиальное представление 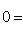
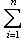
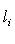 , в котором, скажем,
, в котором, скажем, 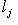
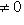 , то
, то 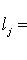
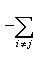
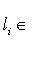
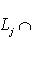
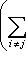
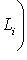 , так что условие а) нарушено. Обращая это рассуждение, получаем, что из нарушения условия а) следует неоднозначность представления нуля.
, так что условие а) нарушено. Обращая это рассуждение, получаем, что из нарушения условия а) следует неоднозначность представления нуля.