Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Нормированные линейные пространства / 1 2 3 4 5 6 7 8 9
Будем называть кругами (соответственно окружностями) в одномерном пространстве L шары (соответственно сферы) ненулевого радиуса с центром в нуле относительно любой из норм. Как следует из предыдущего рассуждения, множества всех кругов и окружностей в L не зависят от выбора исходной нормы. Вместо задания любой нормы можно указать ее единичный круг B или единичную окружность S: S восстанавливается по B как граница B, а B восстанавливается по S как множество точек вида Чтобы перенести это описание на пространства любой размерности, необходимо ввести понятие выпуклости. Подмножество Пусть
т. е. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
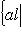
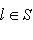
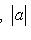
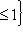 . Заметим, что при
. Заметим, что при 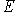
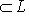 называется выпуклым, если для любых двух векторов
называется выпуклым, если для любых двух векторов 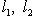
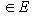 и для любого числа
и для любого числа 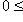
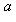
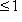 вектор al1 + (1 - a)l2 лежит в E. Это согласуется с обычным определением выпуклости в R2 и R3: вместе с любыми двумя точками ("концами векторов l1 и l2") множество E должно содержать весь соединяющий их отрезок ("концы векторов al1 + (1 - a)l2").
вектор al1 + (1 - a)l2 лежит в E. Это согласуется с обычным определением выпуклости в R2 и R3: вместе с любыми двумя точками ("концами векторов l1 и l2") множество E должно содержать весь соединяющий их отрезок ("концы векторов al1 + (1 - a)l2").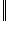
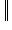 - некоторая норма на L. Положим
- некоторая норма на L. Положим 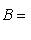
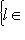

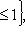
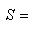
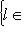
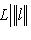
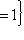 . Ограничение
. Ограничение 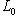
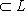 индуцирует норму на L0. Отсюда следует, что для любого одномерного пространства
индуцирует норму на L0. Отсюда следует, что для любого одномерного пространства 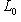
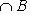 является кругом в L0, а множество
является кругом в L0, а множество 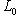
 - окружностью в смысле данного выше определения. Кроме того, из неравенства треугольника следует, что если
- окружностью в смысле данного выше определения. Кроме того, из неравенства треугольника следует, что если 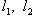
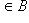 ,
, 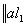
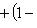
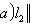
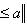
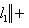
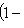
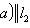
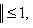
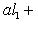
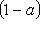
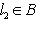 , так что B - выпуклое множество.
, так что B - выпуклое множество.