Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Евклидовы пространства / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
7. Приложения к пространствам функций. Рассмотрим в качестве примера пространство непрерывных вещественных функций на
Оно бесконечномерно, но все наши неравенства будут относиться к конечному числу таких функций, так что каждый раз можно будет считать, что мы работаем в конечномерном евклидовом пространстве: Неравенство Коши-Буняковского-Шварца приобретает вид
Неравенство треугольника:
Если
-1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник


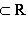 со скалярным произведением
со скалярным произведением



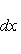
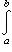
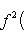

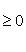 и если
и если 


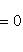 , то
, то 
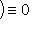 .
.



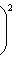


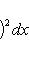





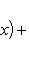

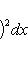
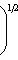

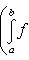
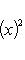


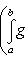


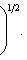
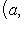


 и ai, bi - коэффициенты Фурье функции f(x), как в
и ai, bi - коэффициенты Фурье функции f(x), как в