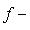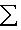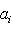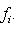Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Алгоритм ортогонализации и ортогональные многочлены / 1 2 3 4 5 6 7 8 9 10 11 12
5. Билинейные формы на пространствах функций. Рассмотрим функции f1, f2, заданные на отрезке (a, b) вещественной прямой (возможно,
или (полуторалинейный случай)
Разумеется, G, f1 и f2 должны удовлетворять каким-то условиям интегрируемости; в последующих примерах они будут выполнены автоматически. Функция G называется весом формы g. Значение
есть взвешенное квадратичное среднее функции f (с весом G); если
|
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
|
|
|
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
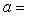
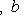
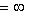 ) и принимающие вещественные или комплексные значения. Пусть G(x) - фиксированная функция от
) и принимающие вещественные или комплексные значения. Пусть G(x) - фиксированная функция от 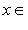
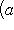
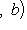 . Билинейные формы на пространствах функций в анализе часто задаются выражениями типа
. Билинейные формы на пространствах функций в анализе часто задаются выражениями типа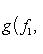
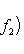
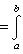
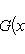
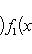
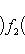
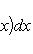
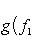
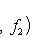
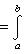
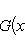
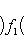
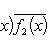
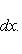
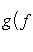
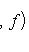

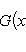
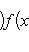
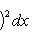 или
или 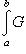
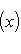
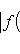
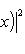
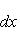
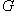
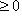 , его можно рассматривать как некоторую интегральную меру уклонения f от нуля. Типичная задача аппроксимации функции f линейными комбинациями некоторого заданного набора функций f1, ..., fn, ... состоит в поиске таких коэффициентов a1, ..., an, ..., которые при данном n минимизируют взвешенное среднее квадратичное функции
, его можно рассматривать как некоторую интегральную меру уклонения f от нуля. Типичная задача аппроксимации функции f линейными комбинациями некоторого заданного набора функций f1, ..., fn, ... состоит в поиске таких коэффициентов a1, ..., an, ..., которые при данном n минимизируют взвешенное среднее квадратичное функции