Cправочник математических формул
Примеры и задачи с решениями
Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
|
Формулы / Дифференциальные уравнения / Линейные обыкновенные дифференциальные уравнения и системы / 1 2 3 4 5 6 7 8
1. В случае
Если
2. В случае
Линейное неоднородное уравнение второго порядка с постоянными коэффициентами
Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения Вид частного решения 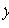 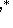 неоднородного уравнения в некоторых конкретных случаях
1. а) число 0 не является корнем характеристического уравнения
где б) число 0 - корень характеристического уравнения, т. е. b = 0, тогда
если 0 - простой корень, т. е.
если 0 - кратный корень, т. е. a = 0. |
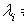
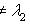
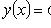
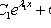
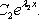
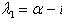
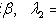
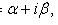то общее решение можно записать и в форме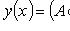
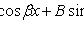
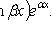
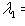
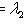
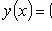
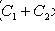
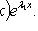
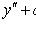
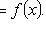
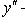
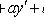
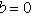и некоторого частного решения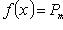 
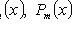- многочлен степени m: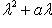
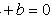, т. е.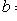 
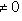, тогда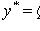
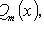
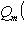
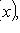- многочлен порядка m;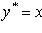
;
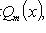
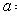
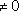