Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
|
Формулы / Бесконечно большие величины / 1 2
4. Бесконечно большая величина предела не имеет. 5. Переменная, принимающая значения, обратные по величине соответственным значениям бесконечно малой величины, есть величина бесконечно большая. 6. Переменная, принимающая значения, обратные по величине соответственным значениям бесконечно большой величины, есть величина бесконечно малая (хотя в некоторых источниках и применяются условные записи 7. Если A постоянная величина, не равная нулю, то произведение A на бесконечно большую величину есть величина бесконечно большая. 8. Произведение двух бесконечно больших величин есть величина бесконечно большая. 9. Отношение бесконечно большой величины к бесконечно малой есть величина бесконечно большая. 10. Сумма двух бесконечно больших величин одинакового знака есть бесконечно большая величина того же знака. 11. Отношение двух бесконечно больших величин не обязательно есть бесконечно большая величина. Это отношение может быть 1) величиной бесконечно большой, 2) величиной конечной и даже 3) величиной бесконечно малой. Об отношениях двух бесконечно больших величин говорят, что оно представляет собой "неопределенность" вида -1-2- |
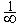 = 0 и
= 0 и 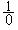 =
= 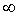 , но их следует всячески избегать, так как 1) делить на нуль запрещено, 2) делить же на
, но их следует всячески избегать, так как 1) делить на нуль запрещено, 2) делить же на 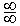 , а отыскание этого отношения называется "раскрытием неопределенности".
, а отыскание этого отношения называется "раскрытием неопределенности".