Cправочник математических формул
Примеры и задачи с решениями

Алфавитный указатель а б в г д е ж з и к л м н о п р с т у ф х ц ч ш щ э ю я
• Примеры решения задач
• Некоторые постоянные
• Элементарная геометрия
• Геометрические преобразования
• Начала анализа и алгебры
• Уравнения и неравенства
• Аналитическая геометрия
• Высшая алгебра
• Дифференциальное исчисление
• Дифференциальная геометрия
• Интегральное исчисление
• Комплексный анализ
• Элементы теории поля
• Тензорное исчисление
• Дифференциальные уравнения
• Математическая логика
• Теория вероятностей и
математическая статистика
Формулы / Бесконечно большие величины / 1 2
Бесконечно большие величины 1. Переменная величина xn называется бесконечно большой, если для всякого наперед заданного числа M > 0 можно указать такое натуральное N, что для всех номеров n, больших N, выполняется неравенство | xn | > M. Короче: переменная величина xn называется бесконечно большой, если, начиная с некоторого номера, она становится и остается при всех последующих номерах по абсолютной величине больше любого наперед заданного положительного числа M. Если xn есть величина бесконечно большая, то это записывается так: lim xn = Следует обратить внимание, что из определения бесконечно большой величины следует, что знак xn роли не играет, а требуется лишь, чтобы абсолютная величина xn, т. е. | xn |, могла быть сделана больше любого наперед заданного положительного числа. Бесконечно большая величина xn называется положительной бесконечно большой величиной, если, начиная с некоторого номера, она становится положительной. В этом случае уже нет надобности писать | xn | > M, знак абсолютной величины (прямые скобки) можно опустить и писать xn > M. В случае, когда xn - положительная бесконечно большая величина, пишут lim xn = + 2. Переменная величина xn называется отрицательной бесконечно большой величиной, если для любого числа M < 0 можно указать такое натуральное число N, что для всех номеров n больших N, выполняется неравенство xn < M. В случае, когда xn - отрицательная бесконечно большая величина, пишут lim xn = - 3. Надо помнить, что символы -1-2- |
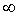 , или xn
, или xn